Another article in which we will introduce the readers to a new metric that will be very useful and completely fair for comparing bowlers from different eras in ODI cricket.
ODI cricket has changed pretty much throughout the years, A total of 200 in the early days would have been a match-winning score, but that same score was now a below-average score, even in average cases current Top ODI teams generally cross 200 around the 40 over the mark and then aim of something around 300 to win the match.
The change is huge and cannot be ignored when comparing two bowlers of completely different generations.
So what to do when we have to compare two bowlers from completely different eras, Joel Garner, with some like Mitchell Starc? Is it fair to compare their numbers as they are; Absolutely. No.
To deal with this, we have a metric in which we will compare the bowler stats with the mean stats of their ERAs to obtain a number (Z-Factor) and then we will use this Z-Factor value to convert the stats of all the bowlers (we are comparing) adjusted towards a particular time period, which will be common for all players.
In the end, we will get Era Adjusted Bowling Average, Economy and Strike Rate which will give us an overview of the Top Bowlers considering the conditions of their ERA.
In your junior classes, you should have read the fundamental concept that for comparing two values with different units, we first have to convert them into the same unit.
This theory is also based on that principle!!
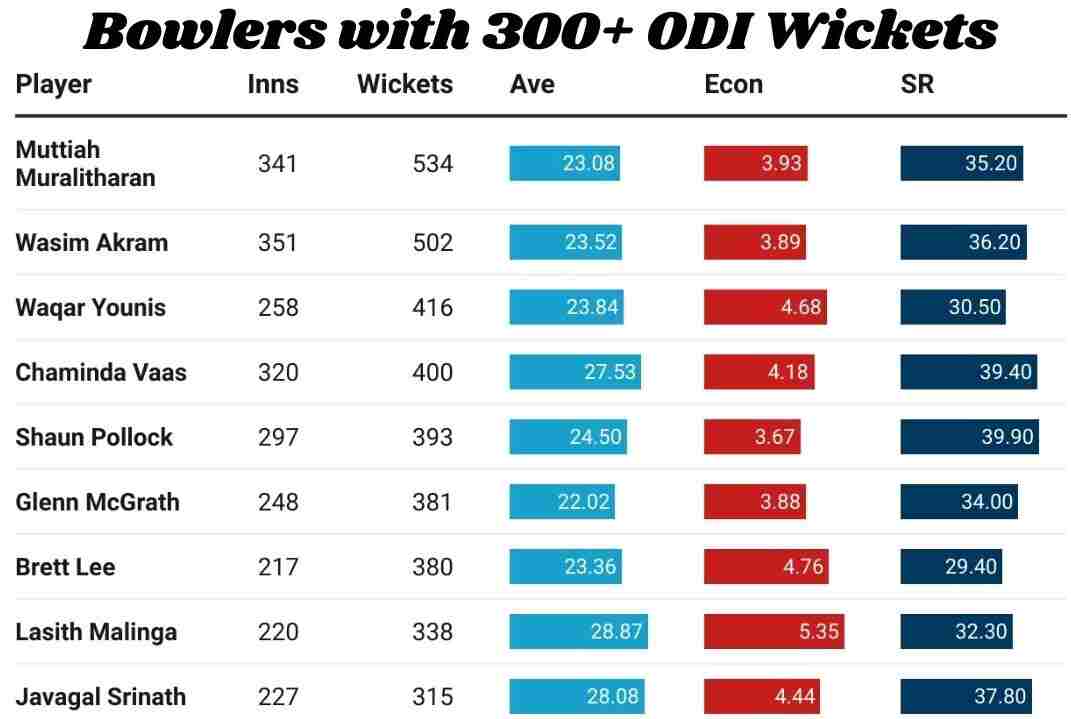
Note: For explaining the metric, I will use the stats of 9 Bowlers, the 9 with at least 300 wickets in ODI cricket.
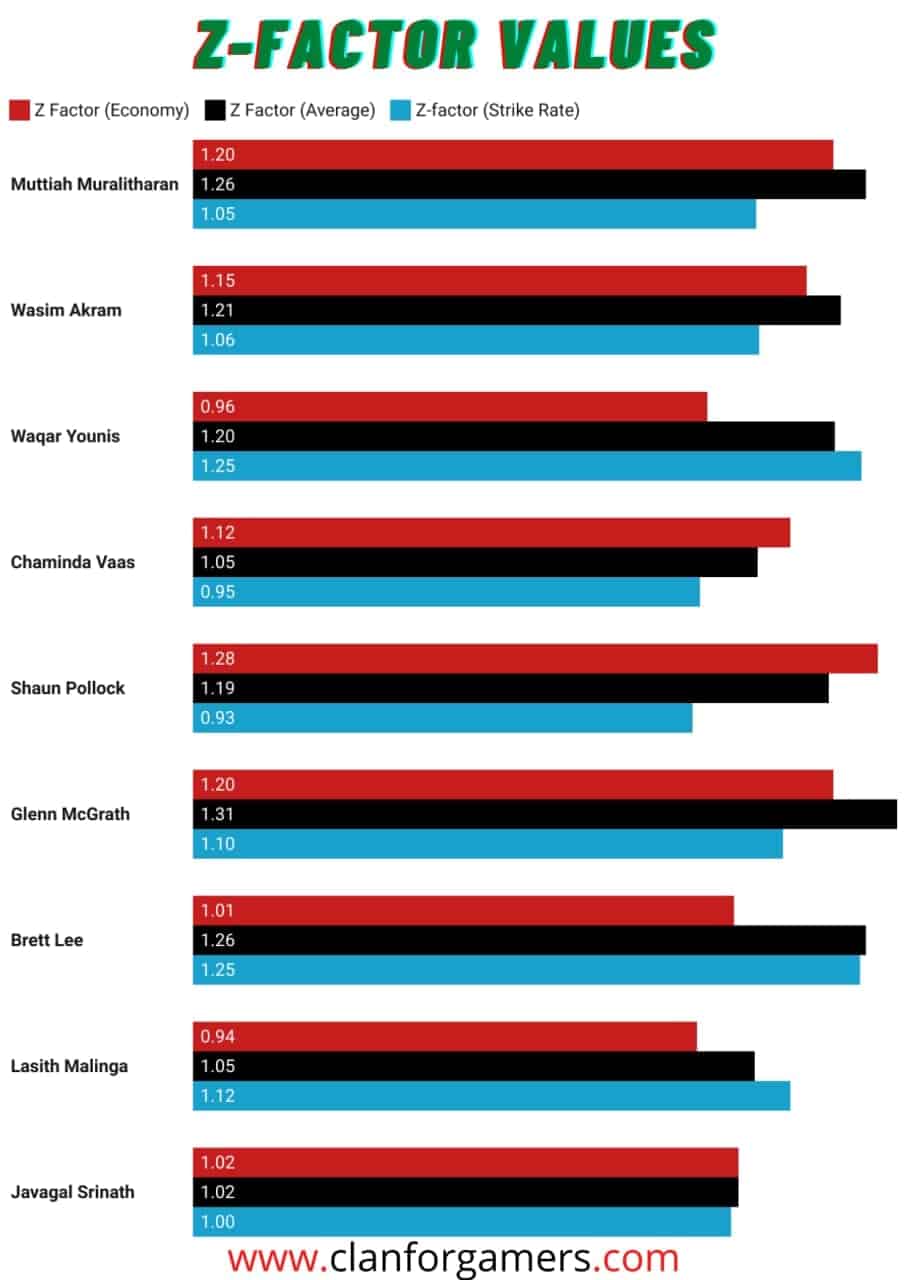
Z-Factor: What is it? How it is calculated?
It’s a simple metric that helps us to get our final results. It is a number that shows how great the player was as compared to the mean credentials of his era.
A value of 1 means, the bowler is as good as an average bowler during his days; A value of 1.2 means his stats were 1.2 times better than the mean stats during his playing days. A number less than 1 means that bowler numbers in a particular metric (avg, eco, sr) are even below the average numbers.
So, the value of the Z-Factor is directly proportional to the player’s dominance in his era.
Now the question will arise; How to calculate the Z-Factor values?
Just divide the mean runs (conceded by a bowler) per wicket of that bowler playing days by the bowler’s bowling average.
Do the same with Economy(RPO) and strike rate (Balls per wicket).
You will get the Z-Factor value of the player’s Bowling average/strike rate/economy.
In simple words, the Z- Factor of a bowler ( Bowling average) is: Mean Bowling Average during his playing days/ His Bowling Average.
For Example, In the case of Wasim Akram, his economy is 3.89, and the mean economy of bowlers during his playing days is 4.45. Then the Z-Factor associated with the economy rate will be 4.46/3.89= 1.15.
Considering the average in this case, Wasim has a bowling average of 23.52 compared to the mean bowling average of 28.42, during his playing days. Z factor for Wasim Bowling Average will be 28.43/23.52=1.2.
His bowling strike rate is 36.2 and if compared to the mean bowling strike rate of his days, which is 38.27, we will obtain the Z-Factor for Wasim Akram Bowling Strike Rate= 38.28/36.2=1.06.
Z-Factor values for these bowlers are given below:
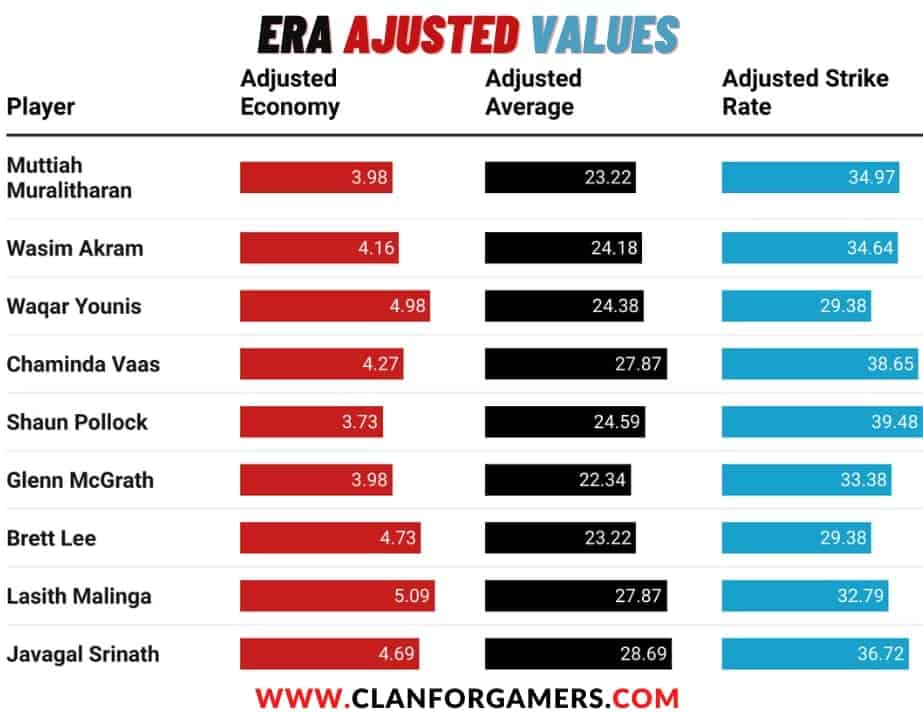
ERA Adjusted Bowling Average, Economy and Strike Rate
Now, as we have these z-factor values for the selected bowlers, to address the query we discussed in the introductory part, we need to present their stats in such a way that they can be compared with ease.
The way to do this is by using these z-factor values to convert bowlers’ (who played in two different generations) stats into stats from a common era.
That means stats of Lasith Malinga, who played from
2004-2019 can be converted in a way that it can be compared to Javagal Srinath, who retired even before the debut of Malinga.
The method to present these stats is quite simple; Just select a random period, 1 January 2000 – 31 December 2010 in our case. Now for all the selected bowlers, we will divide their Z- Factor values from the mean stats for the chosen period.
Mean Bowling Stats during our selected period:
Balls Per Wicket = 36.72
Runs conceded by bowler per Wicket=29.26
Runs conceded by bowler per Over=4.78
Taking the case of Wasim Akram here again; He has a Z-Factor value of 1.15 for the economy, dividing it from the mean economy of our selected time span (4.78), we get 4.78/1.15=4.16.
That can be treated as Wasim’s Economy Rate if he played in our selected time period (01 Jan 2000 – 31 Dec 2009).
Era Adjusted Bowling Average, Economy and Strike Rate of the selected bowlers are given below:
Conclusion/Summary
A point-based summary of what we have discussed in this article is given below:
- How ODI cricket has changed throughout the years.
- Why would comparing the raw stats of two bowlers from different eras be completely unfair?
- Z-Factor
- What is Z-Factor?
- How to calculate it?
- What does it signify?
- Era Adjusted Bowling Average, Economy and Strike Rate
- Why is it a completely fair metric to compare bowlers of two different generations?
- How is it related to Z-Factor?
- How is it calculated?
Z- Factor: A metric to show the domination level, a player has during his playing days.
— Rohit Chhabra (@clanforgamers) February 9, 2022
It is simply, the ratio of the bowler stats with the”mean stats during his era”.
It shows how ahead the bowler was as compared to an average bowler (z -factor value of 1) during his era. pic.twitter.com/WR2YPRY0ZV